본 내용은 임석구, 홍경호 저자의 '최신 컴퓨터 구조'를 참고했음을 알림니다.
1. 논리 게이트
2. 불 대수
1. 논리 게이트
TTL vs CMOS 논리 레벨 정의
TTL : 논리 1 (2.5~5V), 논리 0(0~0.8V)
CMOS : 논리 1 (3.5~5V), 논리 0(0~1.5V)
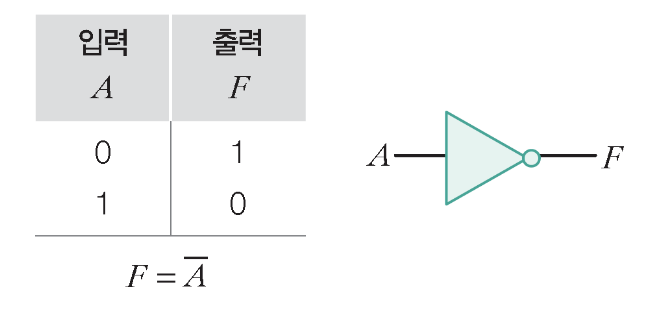
1) NOT 게이트
- 인버터로도 불린다.
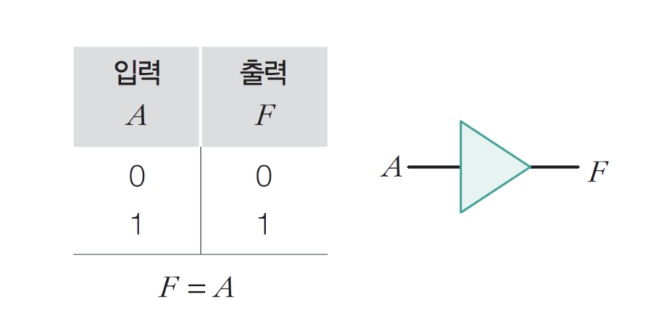
2) 버퍼 게이트
- 단순 전송
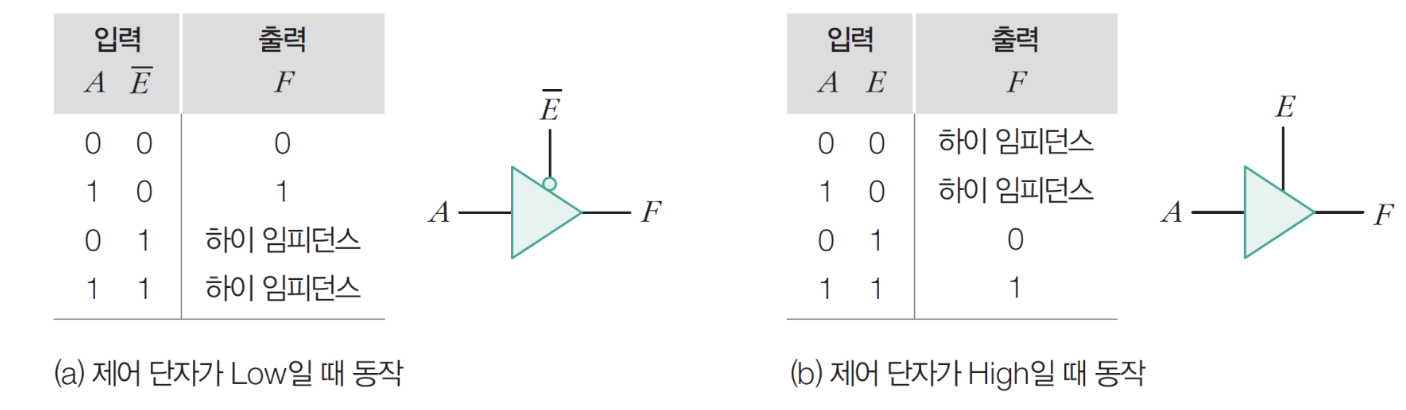
4) 3상태 버퍼 게이트
- 출력이 High, Low, 하이 임피던스 3개 중 하나인 게이트
5) AND 게이트
- 입력이 모두 1이여야 1출력
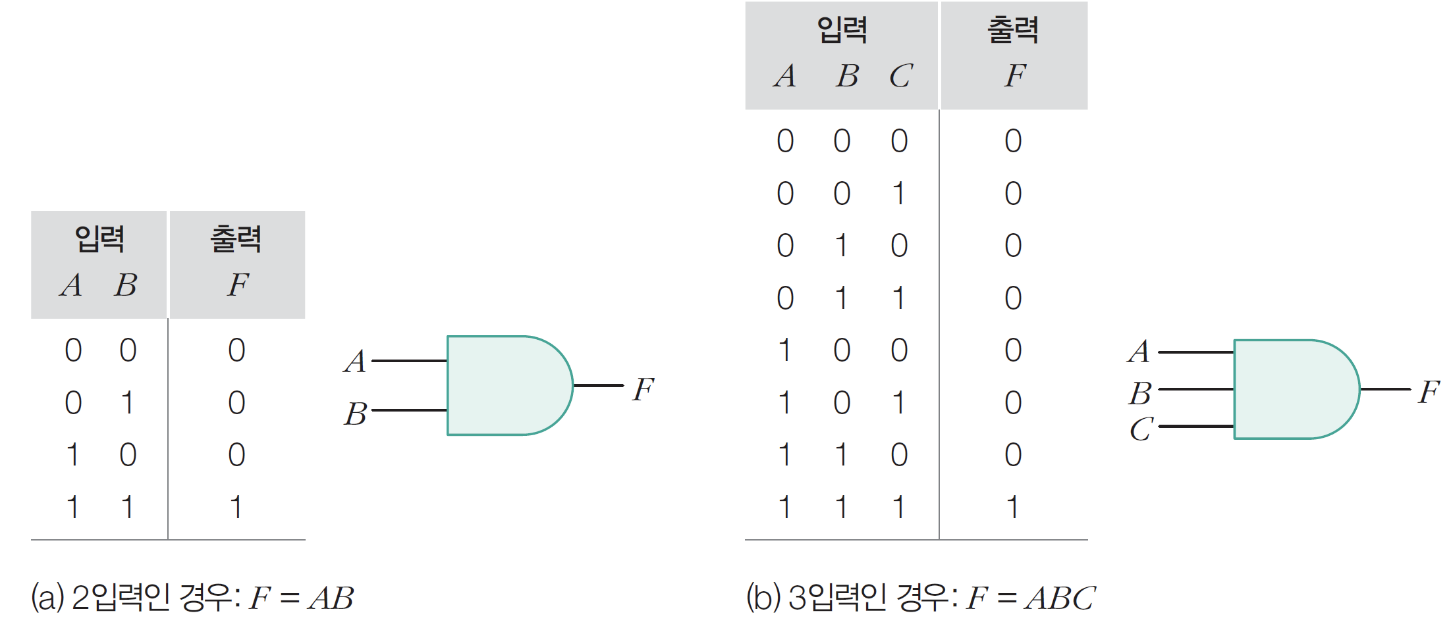
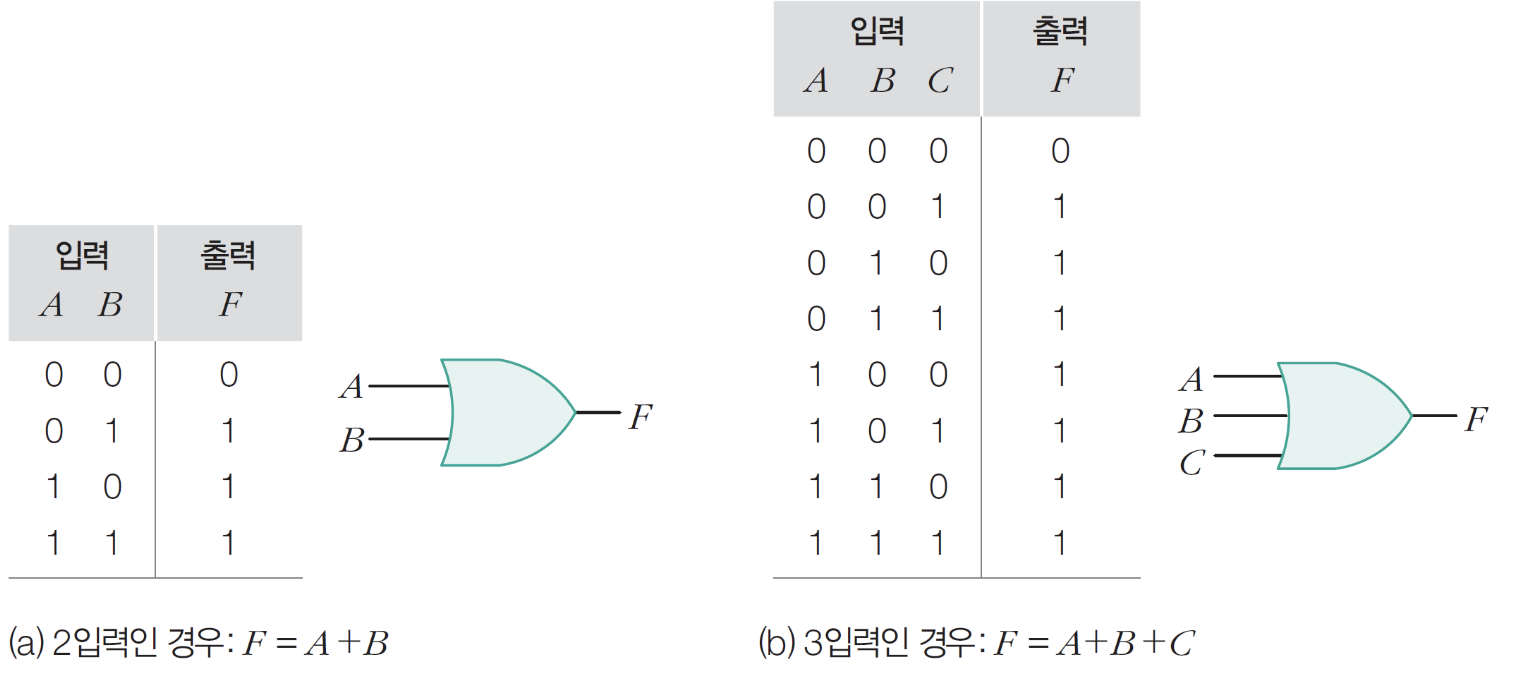
6) OR 게이트
- 입력이 하나라도 1이면 1출력
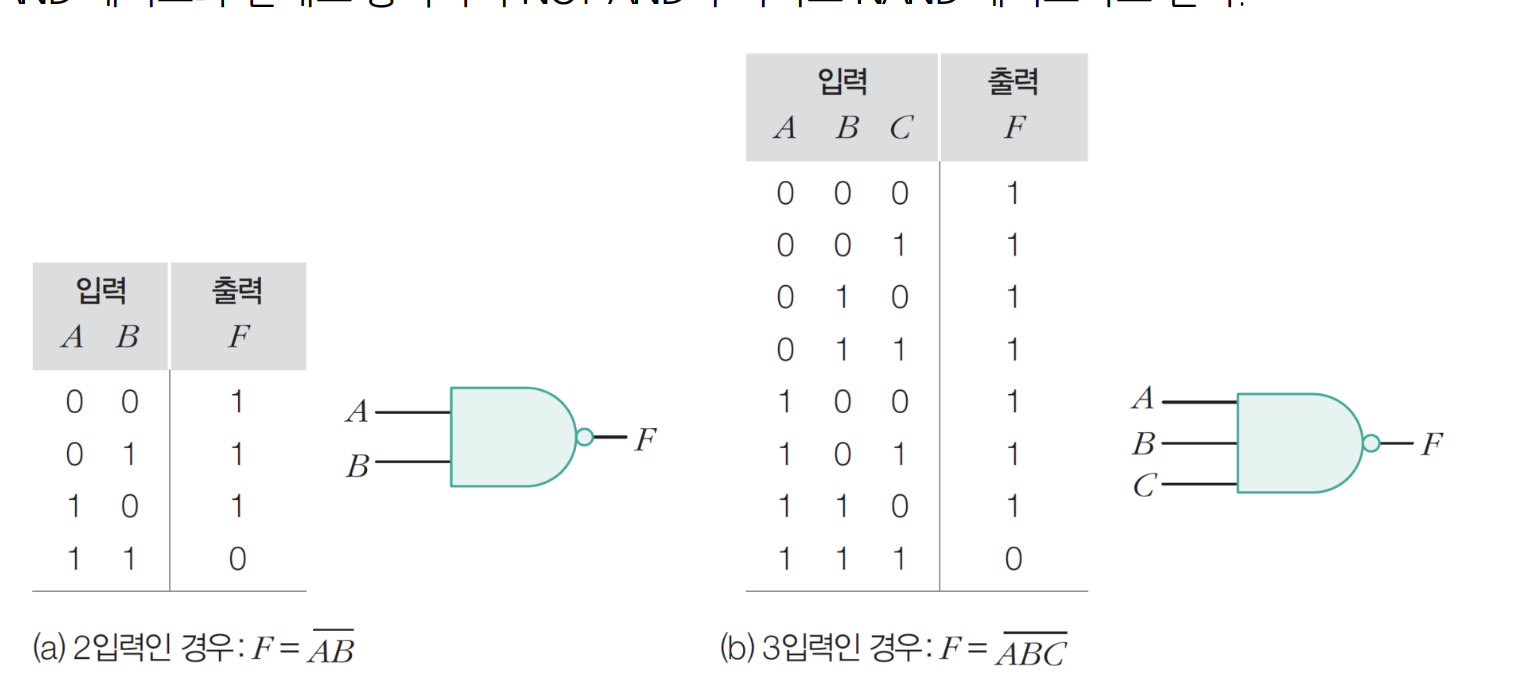
7) NAND 게이트
- 입력이 모두 1이면 0출력
- AND + NOT
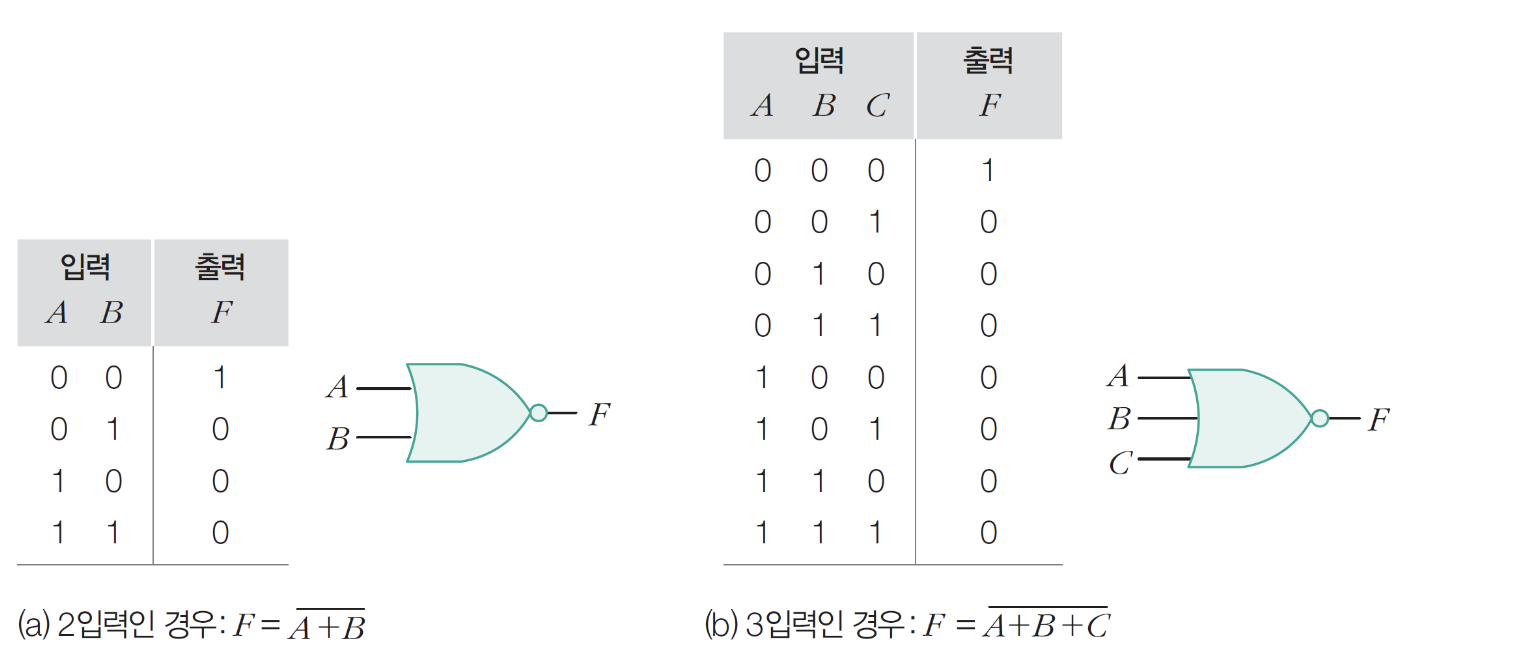
8) NOR 게이트
- 입력이 하나라도 1이면 0출력
- OR + NOT
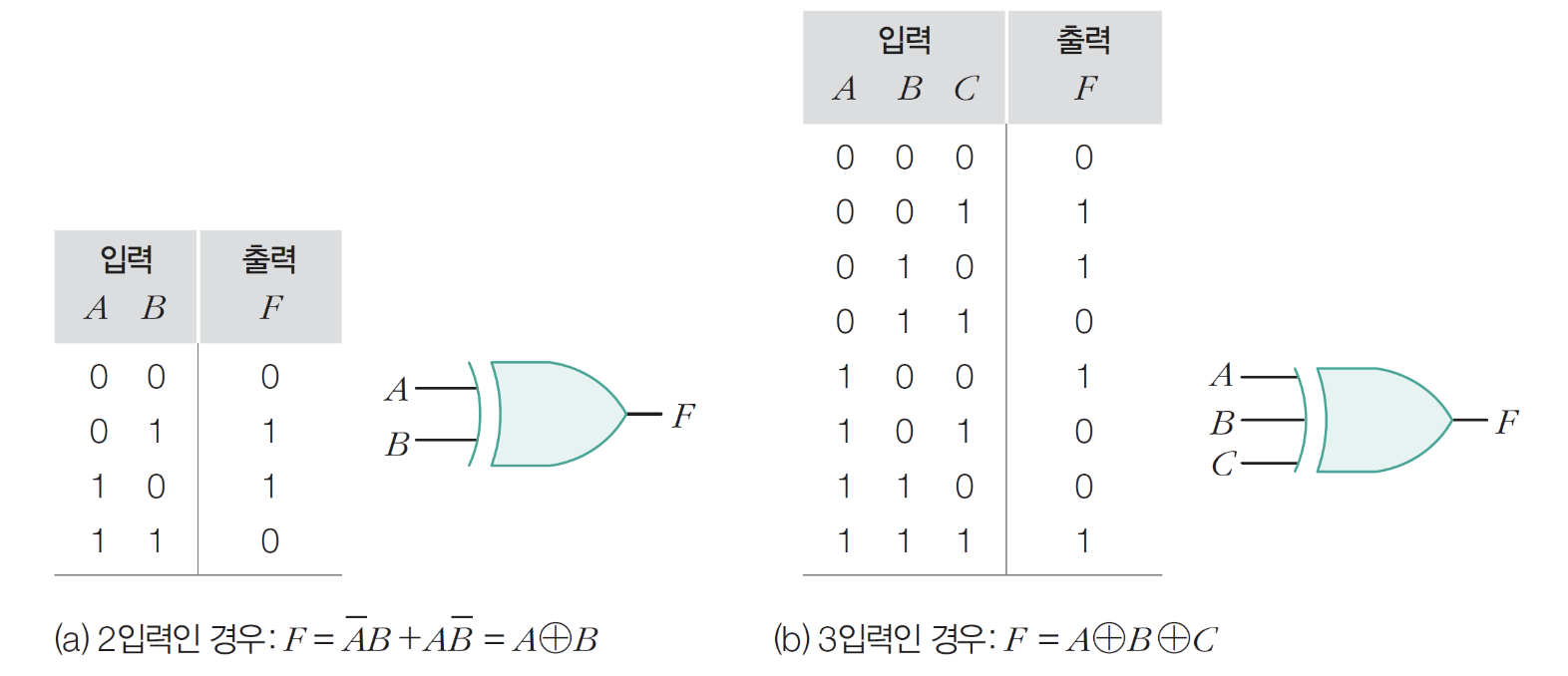
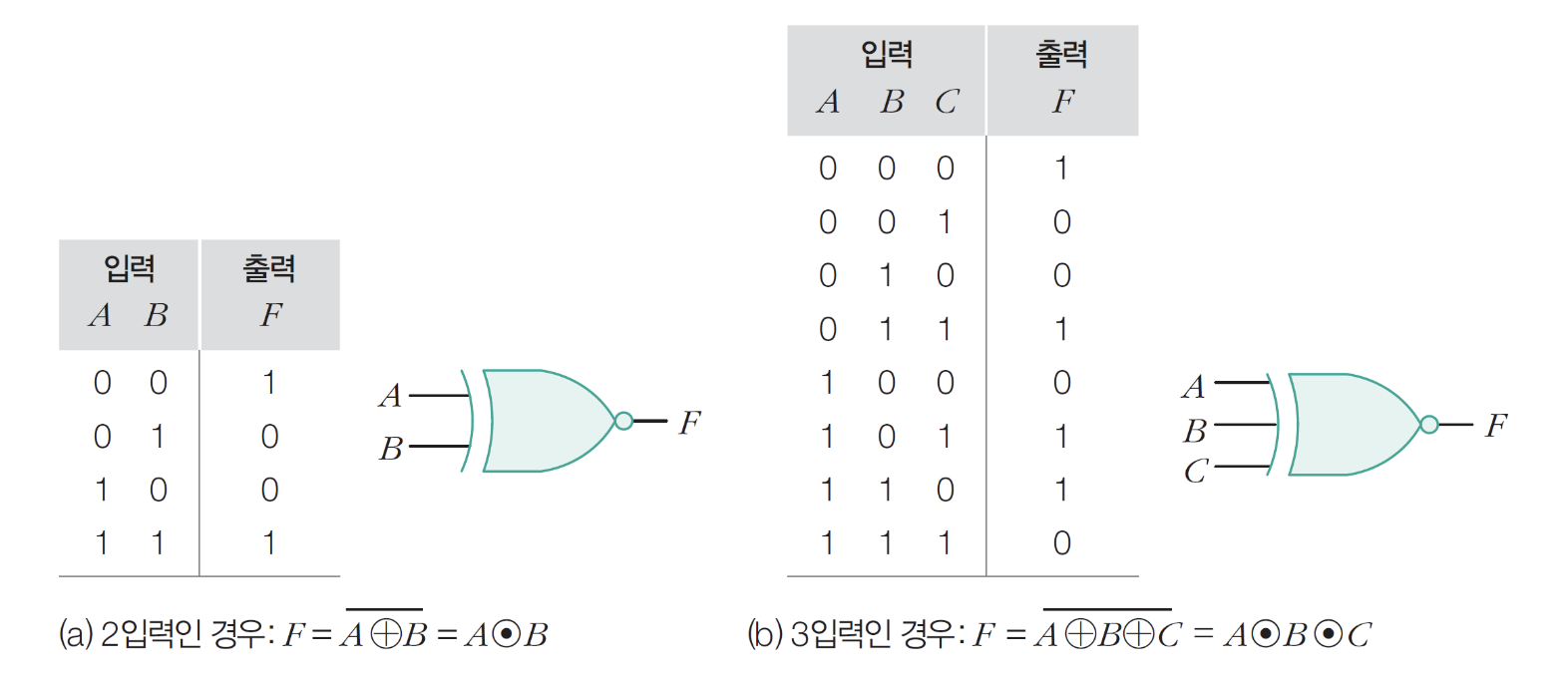
9) XOR 게이트
- 1의 개수가 홀수면 1, 짝수면 0 출력
10) XNOR 게이트
- 1의 개수가 홀수면 0, 짝수면 1 출력
- XOR + NOT
11) 유니버설 게이트
- NAND 와 NOR 게이트 만으로 모든 회로를 만들 수 있기 때문에 이 둘을 유니버설 게이트라고 지칭
11-1) NOT 게이트
- NAND 또는 NOR 게이트의 입력을 하나라 묶으면 NOT 게이트를 만들 수 있다.

11-2) AND 게이트
- F = AB 에서 이중부정해 구현
-> AB = (A'+B')' = AB
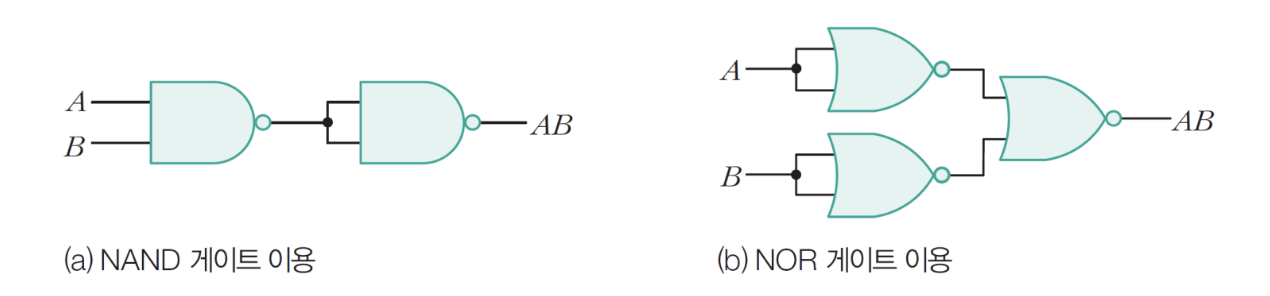
11-3) OR 게이트
- F = A + B 에서 이중부정해 구현
-> A+B = (A'B')' = A+B
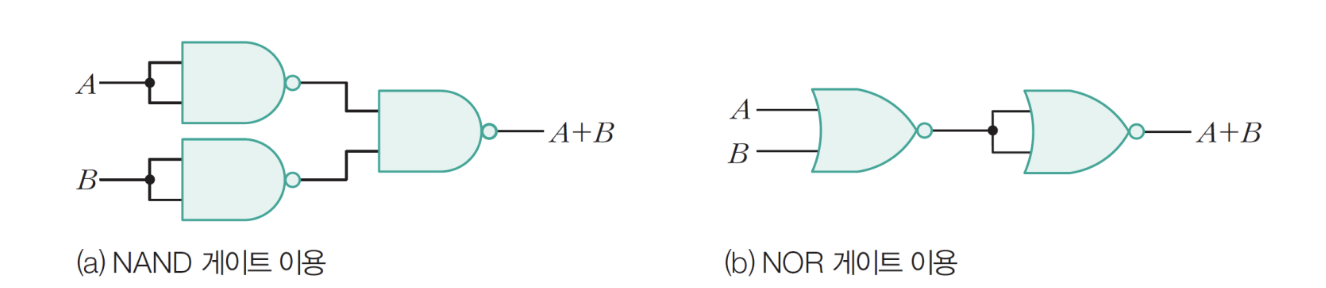
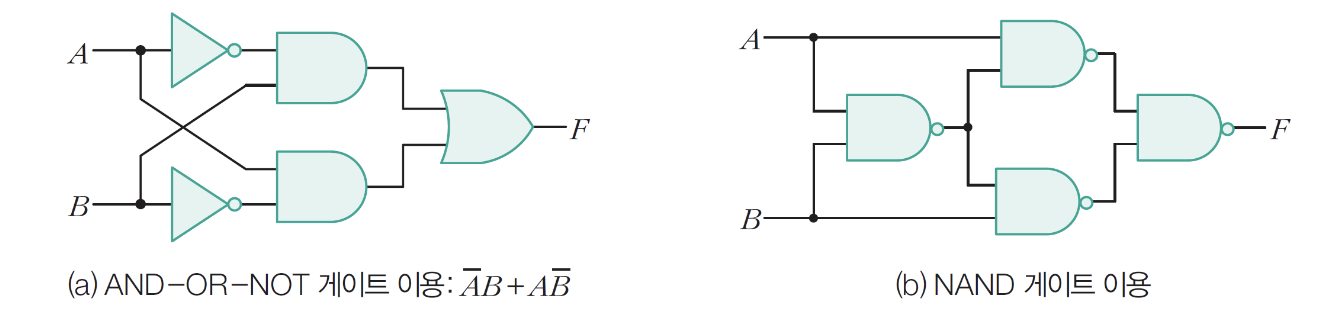
11-4) XOR 게이트
12) 와이어드 로직
- 직접회로(IC)에서는 NAND, NOR 게이트로 구성된다.
- 둘 이상의 NAND 또는 NOR로 연결된 게이트의 출력에 연결해 특정 논리 함수를 수행하는 형태를 와이어드 로직이라고 한다.
2. 불 대수
- AND, OR, NOT을 이용해 볼 대수식을 표현한다.
- AND : x
- OR : +
- NOT : A'
- 기본적으로 교환, 결합이 적용된다.
- 증명은 진리표로 증명한다.
분배 법칙
- A+BC = (A+B)(A+C)
-A(B+C) = AB + AC
드모르간의 정리
(A+B)' = A'B'
(AB)' = A'+B'
흡수 법칙
A + AB = A
A(A+B) = A
합의 정리
AB + BC + A'C = AB + A'C
(A+B)(B+C)(A'+C) = (A+B)(A'+C)
볼 대수식의 표현 형태
1) 곱의 합과 최소항
1-1) 곱의 합
- 1단계 입력은 AND, 2단계 입력은 OR로 구성된 논리식을 의미한다.
1-2) 최소항
- 입력 00, 01, 10, 11 을 기호로 표현한다.
- 입력이 0이면 NOT으로 표현
00 - A'B'
01 - A'B
10 - AB'
11 - AB
1-3) 최소항 식
- 출력이 1이 되는 항의 변수를 AND 연산하고, 각 항을 OR 연산하는 식이다.

2) 합의 곱과 최대 항
2-1) 합의 곱
- 1단계 입력이 OR, 2단계 입력이 AND로 만들어진 논리 식을 의미한다.
2-2) 최대 항
- 입력 00, 01, 10, 11을 기호로 표현한다.
- 최소항과 반대로 표현
- 입력이 1이면 NOT으로 표현
00 - A+B
01 - A+B'
10 - A'+B
11 - A'+B'
2-3) 최대항 식
- 출력이 0이되는 입력변수를 OR처리 후 모두 AND처리하는 방식이다.

정리
- 최대항과 최소항은 서로 보수의 성질을 띤다. (서로 부정 관계)
논리식의 간소화
1) 볼 대수 법칙을 이용한다.
2) 카르노 맵을 이용한다.
3) 도표법을 이용한다.
카르노 맵
- 최소항을 사용한다. (입력이 0이면 NOT으로 표현)
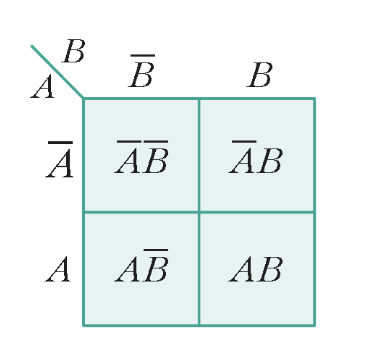


규칙
1. 이웃하는 최소항끼리 묶는다.
2. 묶는 단위는 1, 2, 4, 8, 16 단위로 묶는다.
3. 직, 정사각형으로 묶고 대각선은 불가능하다.
4. 최대한 크게 묶는다.
5. 중복해서 묶는 것이 더 간소하다면 중복해서 묶는다.
6. 무관항이 간소화될 수 있으면 묶어 주고, 그렇지 않으면 묶지 않는다.
무관항
- 입력이 0이든 1이든 상관없는, 즉, 입력이 결과에 영향을 끼치지 않는 최소항을 의미.
- x나 d로 표시한다.
XOR와 XNOR의 카르노 맵
- 카르노 맵에서 그룹으로 묶은 후 제거되는 변수를 제외한 다른 입력 변수의 1의 개수가 홀수라면 XOR, 짝수면 XNOR을 의미한다.
'CS Knowledge > Computer Structure' 카테고리의 다른 글
| Computer Structure - CPU(2) (0) | 2023.04.18 |
|---|---|
| Computer Structure - CPU(1) (0) | 2023.04.17 |
| Computer Structure - Digital Logic Circuits(2) (0) | 2023.04.17 |
| Computer Structure - Data Expression (1) | 2023.04.16 |
| Computer Structure - Basic (1) | 2023.04.16 |



